《梦溪笔谈》中的隙积术

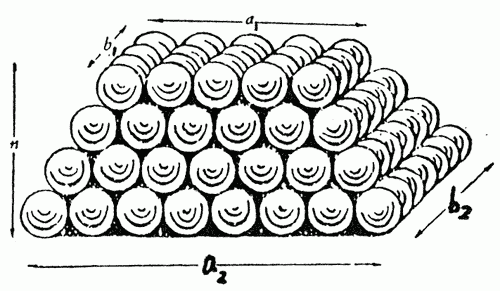
笔记提到的"有隙者如累累層壇及酒家積罌(酒坛)",描述的是酒坛、棋子等物体堆积时存在的空隙问题。传统"刍童"(梯形棱台)体积公式(长×宽×高)无法精确计算此类离散堆积体的实际数量。沈括的突破:在"刍童体积公式"基础上增加修正项: 总数 = (上层长×上层宽 + 下层长×下层宽 + 上层长×下层宽 + 上层宽×下层长) × 高 / 6 + 高×(下宽 - 上宽)/6 文本中的"以高乘之,六而二"(高²/6)即修正项的关键部分。 通过"倍上長加入下長"等步骤,将连续型转化为离散求和公式,解决阶坛、酒坛堆积等实际问题。
会圆术
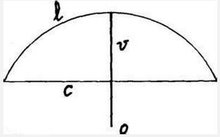
首 创由弦长(a)和矢高(h)求弧长的近似公式,比欧洲同类方法早400余年。核心思想为以直代曲的实用化 沈括将圆弧分割为若干直线段,用勾股定理进行近似计算,体现了“局部线性化”思想。这种方法简化了复杂几何问题,使实际工程(如土地测量、天文历法)中的弧长计算成为可能。此方法当圆心角小于45°时,相对误差小于2%实用性极强。
不同于传统数学的抽象演绎,沈括强调从实际问题出发推导公式。例如,他通过调整“古法”(中破圆法)的误差,提出更精确的解决方案,反映了宋代科学注重实证的特点。沈括的“以简驭繁”思想(如简化复杂几何问题)启发了后世数学家,成为中国古代数学从算法向理论模型过渡的标志性成果。元代郭守敬在《授时历》中直接应用会圆术计算天体运动轨迹,标志着其从理论到实践的成功转化。
原文(节选): “余别为拆会之术,置圆田,径半之以为弦,又以半径减去所割数,余者为股;各自乘,以股除弦,余者开方除为勾,倍之为割田之直径。以所割之数自乘倍之,又以圆径除所得,加入直径,为割田之弧。” ——《梦溪笔谈》卷十八《技艺》
已知条件:圆田直径(D)、弧高(h,即矢高)。 步骤: 将直径的一半(半径r = D/2)作为直角三角形的斜边(弦)。 弧高h = 半径r - 股长(即r - h)。 通过勾股定理计算弦长(a = 2√(r² - (r - h)²))。 弧长近似公式:弧长 ≈ a + (2h²)/D。